Kirchhoff's Laws: Complete Guide with Circuit Analysis Examples & Calculations

Kirchhoff's Laws are fundamental principles in electrical engineering that every student and professional must master for effective circuit analysis. These two simple yet powerful laws - Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL) - provide the foundation for solving complex electrical networks and are essential for understanding how current flows and voltage distributes in electrical circuits.

Whether you're designing power distribution systems, analyzing electronic circuit designs, or working with AC circuit analysis, Kirchhoff's Laws are your go-to tools for accurate calculations and reliable results.

Understanding Kirchhoff's Laws: The Foundation of Circuit Analysis

Kirchhoff's Laws consist of two fundamental principles that govern electrical circuits:

1. Kirchhoff's Current Law (KCL) - Node Analysis

Statement: The algebraic sum of all currents entering and leaving any node (junction) in a circuit equals zero.

Mathematical Expression: $\sum I_{\text{node}} = 0$

Or alternatively: $\sum I_{\text{in}} = \sum I_{\text{out}}$

Physical Basis: Based on the conservation of electric charge - charge cannot accumulate at any point in a circuit.

2. Kirchhoff's Voltage Law (KVL) - Loop Analysis

Statement: The algebraic sum of all voltage drops and rises around any closed loop in a circuit equals zero.

Mathematical Expression: $\sum V_{\text{loop}} = 0$

Physical Basis: Based on the conservation of energy - the energy gained by a charge moving around a closed loop must equal the energy lost.

Step-by-Step Circuit Analysis Using Kirchhoff's Laws

Example 1: Simple Series-Parallel Circuit Analysis

Let's solve a practical circuit with the following components:

• Voltage source: V = 12V
• Resistor R₁ = 4Ω (series)
• Resistor R₂ = 6Ω (parallel branch)
• Resistor R₃ = 3Ω (parallel branch)

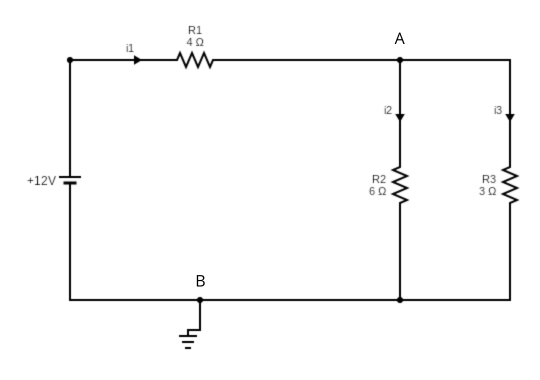
Step 1: Identify Nodes and Loops

• Node A: Junction where R₁ connects to parallel branches
• Node B: Common ground point
• Loop 1: V - R₁ - R₂ (through R₂ branch)
• Loop 2: R₂ - R₃ (between parallel branches)

Step 2: Apply KCL at Node A

Let's define:

• I₁ = current through R₁
• I₂ = current through R₂
• I₃ = current through R₃

Applying KCL at Node A: $I_1 = I_2 + I_3$

Step 3: Apply KVL in Loop 1

Going clockwise around Loop 1:

$$12V - I_1(4Ω) - I_2(6Ω) = 0$$ $$12 - 4I_1 - 6I_2 = 0 \tag{1}$$

Step 4: Apply KVL in Loop 2

Around the parallel branch loop:

$$I_2(6Ω) - I_3(3Ω) = 0$$ $$6I_2 - 3I_3 = 0$$ $$I_3 = 2I_2 \tag{2}$$

Step 5: Solve the System of Equations

Substituting Equation 2 into the KCL equation: $I_1 = I_2 + 2I_2 = 3I_2$

Substituting into Equation 1:

$$12 - 4(3I_2) - 6I_2 = 0$$ $$12 - 12I_2 - 6I_2 = 0$$ $$12 = 18I_2$$ $$I_2 = \tfrac{12}{18} = 0.667A$$

Therefore:

• I₂ = 0.667A
• I₃ = 2 × 0.667 = 1.333A
• I₁ = 3 × 0.667 = 2A

Step 6: Verify Using Power Balance

Total power supplied: P = VI₁ = 12V × 2A = 24W

Power dissipated:

• P₁ = I₁²R₁ = (2)² × 4 = 16W
• P₂ = I₂²R₂ = (0.667)² × 6 = 2.67W
• P₃ = I₃²R₃ = (1.333)² × 3 = 5.33W
• Total = 16 + 2.67 + 5.33 = 24W ✓

Example 2: Complex Multi-Loop Circuit

Mesh Analysis Using Kirchhoff's Voltage Law (KVL)

Mesh analysis is a systematic method for solving electrical circuits using Kirchhoff's Voltage Law (KVL). This technique is particularly useful for circuits with multiple loops and current sources.

Circuit Analysis Example

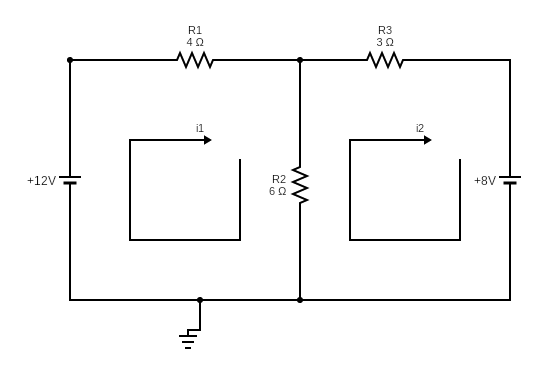
Let's analyze a two-mesh circuit with multiple voltage sources and resistors to demonstrate the complete mesh analysis process.

Given Circuit Parameters:

• V₁ = 12V (voltage source)
• V₂ = 8V (voltage source)
• R₁ = 4Ω (resistor)
• R₂ = 6Ω (resistor)
• R₃ = 3Ω (resistor)

Step 1: Identify Meshes and Assign Mesh Currents

We have two meshes in this circuit:

• Mesh 1 (i₁): Left loop containing V₁, R₁, and R₂
• Mesh 2 (i₂): Right loop containing R₂, V₂, and R₃

Both mesh currents are assumed to flow clockwise.

Step 2: Apply KVL to Mesh 1

Starting from the top and going clockwise:

• Voltage rises: +V₁ = +12V
• Voltage drops: -i₁R₁ - (i₁ - i₂)R₂

Applying KVL: $V_1 - i_1R_1 - (i_1 - i_2)R_2 = 0$

Substituting the given values: $12 - 4i_1 - 6(i_1 - i_2) = 0$

Expanding: $12 - 4i_1 - 6i_1 + 6i_2 = 0$

Simplifying:

$$12 - 10i_1 + 6i_2 = 0 \tag{Equation 1}$$

Step 3: Apply KVL to Mesh 2

Starting from the top and going clockwise:

• Voltage rises: +V₂ = +8V
• Voltage drops: -(i₂ - i₁)R₂ - i₂R₃

Applying KVL: $(i_2 - i_1)R_2 + V_2 - i_2R_3 = 0$

Substituting the given values: $6(i_2 - i_1) + 8 - 3i_2 = 0$

Expanding: $6i_2 - 6i_1 + 8 - 3i_2 = 0$

Simplifying:

$$-6i_1 + 3i_2 + 8 = 0 \tag{Equation 2}$$

Step 4: Solve the System of Equations

We now have two equations with two unknowns:

$$12 - 10i_1 + 6i_2 = 0 \tag{1}$$ $$-6i_1 + 3i_2 + 8 = 0 \tag{2}$$

Rearranging:

• From equation (1): $10i_1 - 6i_2 = 12$
• From equation (2): $6i_1 - 3i_2 = 8$

Multiply equation (2) by 2:

$$12i_1 - 6i_2 = 16 \tag{3}$$

Subtract equation (1) from equation (3):

$$(12i_1 - 6i_2) - (10i_1 - 6i_2) = 16 - 12$$ $$2i_1 = 4$$ $$i_1 = 2\text{ A}$$

Substitute $i_1 = 2$ into equation (1):

$$10(2) - 6i_2 = 12$$ $$20 - 6i_2 = 12$$ $$6i_2 = 8$$ $$i_2 = \frac{4}{3}\text{ A} ≈ 1.33\text{ A}$$

Step 5: Calculate Individual Branch Currents

Now we can determine the current through each component:

Component	Current	Voltage Drop
R₁	$i_1 = 2$ A	$V_{R1} = 2 × 4 = 8$ V
R₂	$i_1 - i_2 = 2 - \frac{4}{3} = \frac{2}{3}$ A	$V_{R2} = \frac{2}{3} × 6 = 4$ V
R₃	$i_2 = \frac{4}{3}$ A	$V_{R3} = \frac{4}{3} × 3 = 4$ V

Solution Verification

Let's verify our solution by checking both KVL equations:

Mesh 1 verification: $12 - (2)(4) - (2 - \frac{4}{3})(6) = 12 - 8 - (\frac{2}{3})(6) = 12 - 8 - 4 = 0 \checkmark$

Mesh 2 verification: $(\frac{4}{3} - 2)(6) + 8 - (\frac{4}{3})(3) = (-\frac{2}{3})(6) + 8 - 4 = -4 + 8 - 4 = 0 \checkmark$

Both equations are satisfied, confirming our solution is correct!

Final Results

• Mesh Current 1 (i₁): 2 A (clockwise)
• Mesh Current 2 (i₂): 4/3 A ≈ 1.33 A (clockwise)
• Current through R₁: 2 A (left to right)
• Current through R₂: 2/3 A ≈ 0.67 A (top to bottom)
• Current through R₃: 4/3 A ≈ 1.33 A (right to left)

Key Points to Remember

1. Consistent Direction: Always define mesh currents consistently (all clockwise or all counterclockwise)
2. Shared Components: For shared resistors, the current is the algebraic sum of mesh currents
3. Voltage Sources: Add positive voltage when traversed from + to - terminal
4. Resistor Drops: Always have voltage drops in the direction of current flow
5. Verification: Always verify your solution by substituting back into the original equations

Applications and Benefits

Mesh analysis is particularly effective for:

• Circuits with multiple voltage sources
• Planar circuits (can be drawn without crossing wires)
• When you need to find mesh currents directly
• Academic and theoretical circuit analysis

Advanced Applications of Kirchhoff's Laws

1. AC Circuit Analysis

When working with alternating current circuits, Kirchhoff's Laws apply to:

• Instantaneous values: KCL and KVL hold at every instant
• Phasor analysis: Using complex numbers for sinusoidal steady-state
• RMS values: For power calculations in AC systems

2. Nodal Voltage Method

This systematic approach uses KCL primarily:

Steps for Nodal Analysis:

1. Select reference node (ground)
2. Identify node voltages
3. Apply KCL at each non-reference node
4. Express currents using Ohm's law
5. Solve resulting equations

3. Mesh Current Method

This approach uses KVL primarily:

Steps for Mesh Analysis:

1. Identify all meshes (loops)
2. Assign mesh currents
3. Apply KVL around each mesh
4. Express voltages using Ohm's law
5. Solve for mesh currents

Practical Applications in Electrical Engineering

Power Distribution Systems

In electrical power systems, Kirchhoff's Laws ensure:

• Load balancing across distribution networks
• Fault analysis in transmission lines
• Power flow calculations in electrical grids

Electronic Circuit Design

For electronic components and circuit design:

• Amplifier analysis using operational amplifiers
• Filter circuit design for signal processing
• Digital logic circuits and microcontroller interfacing

Circuit Simulation and Analysis

Modern circuit simulation software like SPICE uses Kirchhoff's Laws as the foundation for:

• SPICE modeling of electronic circuits
• Transient analysis for time-domain behavior
• Frequency response analysis

Troubleshooting Common Circuit Problems

Problem-Solving Strategy

1. Identify the circuit topology (series, parallel, or combination)
2. Choose analysis method (nodal or mesh analysis)
3. Apply appropriate Kirchhoff's Law
4. Set up equations systematically
5. Solve and verify results

Circuit Analysis Comparison Table

Method	Primary Law Used	Best For	Variables Solved
Nodal Analysis	KCL (Current Law)	Circuits with fewer nodes	Node voltages
Mesh Analysis	KVL (Voltage Law)	Circuits with fewer loops	Loop currents
Branch Analysis	Both KCL & KVL	Simple circuits	Branch currents/voltages
Superposition	Both (applied separately)	Multi-source circuits	Individual source effects

Advanced Circuit Analysis Techniques

Thévenin and Norton Equivalent Circuits

Using Kirchhoff's Laws with Thévenin's theorem:

• Simplify complex networks
• Analyze load variations
• Design matching networks

Superposition Principle

When dealing with multi-source circuits:

• Apply Kirchhoff's Laws to each source individually
• Sum the individual responses
• Verify using complete circuit analysis

Real-World Circuit Examples

Example 3: LED Circuit Analysis

For LED circuit design:

• Forward voltage drop: V_LED = 2.2V
• Supply voltage: V_s = 9V
• Desired current: I_LED = 20mA
• Required resistance: R = (9V - 2.2V) / 0.02A = 340Ω

Example 4: Battery Charging Circuit

In battery management systems:

• Apply KVL to determine charging current
• Use KCL for current distribution in parallel battery banks
• Calculate power dissipation in charging resistors

Circuit Analysis Software and Tools

Modern electrical engineers use various tools that implement Kirchhoff's Laws:

1. LTSpice - Free SPICE simulator
2. Multisim - Educational circuit simulation
3. PSpice - Professional circuit analysis
4. MATLAB Simulink - System-level modeling
5. KiCad - Open-source PCB design with simulation

These tools automate the application of Kirchhoff's Laws for complex circuits with hundreds or thousands of components.

Best Practices for Circuit Analysis

1. Systematic Approach

• Always define current directions and voltage polarities clearly
• Use consistent sign conventions throughout the analysis
• Label all nodes and components systematically

2. Verification Methods

• Check that KCL is satisfied at each node
• Verify that KVL equals zero around each loop
• Confirm power balance (power supplied = power consumed)

3. Common Pitfalls to Avoid

• Mixing up current directions in KCL equations
• Incorrect voltage polarity in KVL loops
• Forgetting to include all circuit elements
• Using dependent variables without establishing relationships

Conclusion: Mastering Circuit Analysis with Kirchhoff's Laws

Kirchhoff's Current and Voltage Laws remain the cornerstone of electrical circuit analysis, providing the theoretical foundation for understanding everything from simple resistor circuits to complex power electronic systems. Whether you're working on Arduino projects, designing PCB layouts, or analyzing industrial electrical systems, these fundamental laws will guide your analysis and ensure accurate results.

The key to mastering circuit analysis lies in consistent practice with increasingly complex circuits, understanding when to apply each law, and developing the ability to set up and solve systems of equations efficiently. With the step-by-step examples and practical applications covered in this guide, you now have the tools to tackle any circuit analysis challenge with confidence.

Ready to advance your electrical engineering skills? Explore our comprehensive guides on advanced circuit analysis and electrical engineering fundamentals to deepen your understanding of these essential concepts.

---

🔗 Related Posts

• Electric Current: A Comprehensive Guide
• Electrical Resistance and How to Calculate It
• Mastering PCB Design and Techniques Wire size Calculator - complete guide

Helpful Calculators

• Resistor Color Code Calculator
• Series Parallel Resistance Calculator
• Ohm's Law Calculator
• Voltage Drop Calculator

Credits

  - Photo by Chris Ried on Unsplash