Understanding Electrical Resistance: Complete Guide with Calculations and Real-World Examples

Have you ever wondered why your smartphone charger gets warm when charging, or why some electrical devices need thicker wires than others? The answer lies in a fundamental electrical property called resistance - a concept that governs how electrical current flows through every circuit, from the simplest flashlight to complex industrial systems.

Understanding electrical resistance is essential for anyone working with electronics, designing circuits, or simply wanting to grasp how electricity behaves in the real world. This guide will teach you not just what resistance is, but how to calculate it, measure it, and apply it to solve practical electrical problems.

Whether you're an engineering student, electronics hobbyist, or professional electrician, mastering resistance calculations will help you design better circuits, troubleshoot problems effectively, and understand why electrical systems behave the way they do.

What is Electrical Resistance?

Electrical resistance is the opposition that a material presents to the flow of electric current. Think of it like friction in mechanical systems - just as friction opposes motion, resistance opposes the flow of electrons through a conductor.

When electrons move through any material, they collide with atoms, impurities, and crystal boundaries. These collisions convert some of the electrical energy into heat energy, which is why resistors get warm and why power lines lose energy over long distances.

The Mathematical Foundation: Ohm's Law

The relationship between voltage, current, and resistance is described by Ohm's Law:

$$V = I \times R$$

Where:

• V = Voltage (volts)
• I = Current (amperes)
• R = Resistance (ohms, Ω)

This can be rearranged to solve for any variable:

• Current: $I = \frac{V}{R}$
• Resistance: $R = \frac{V}{I}$

Power Dissipation in Resistive Elements

When current flows through resistance, electrical energy is converted to heat. The power dissipated is calculated using:

$P = I^2 \times R = \frac{V^2}{R} = V \times I$

Key insight: Power increases with the square of current, making current the most critical factor in heating calculations.

Factors That Determine Resistance

1. Material Properties (Resistivity)

Different materials have inherently different abilities to conduct electricity, quantified by their resistivity (ρ):

Material	Resistivity (Ω·m)	Application
Silver	1.59 × 10⁻⁸	Premium contacts
Copper	1.68 × 10⁻⁸	Standard wiring
Aluminum	2.82 × 10⁻⁸	Power transmission
Iron	9.71 × 10⁻⁸	Magnetic applications
Nichrome	1.10 × 10⁻⁶	Heating elements
Carbon	3.50 × 10⁻⁵	Resistors

2. Physical Dimensions

The resistance of any conductor depends on its geometry according to:

$$R = \rho \times \frac{L}{A}$$

Where:

• ρ = Material resistivity
• L = Length of conductor
• A = Cross-sectional area

Practical implications:

• Longer conductors: Higher resistance
• Thicker conductors: Lower resistance
• Material choice: Dramatically affects resistance

3. Temperature Effects

Most materials' resistance changes with temperature. For metals, the relationship is approximately linear:

$$R_T = R_{20} \times [1 + α \times (T - 20°C)]$$

Where:

• $R_T$ = Resistance at temperature T
• $R_{20}$ = Resistance at 20°C
• α = Temperature coefficient (0.004/°C for copper)

Step-by-Step Resistance Calculations

Example 1: Basic Circuit Analysis

Given: 12V battery connected to a 4Ω resistor

Step 1 - Calculate Current (Ohm's Law): $I = \frac{V}{R} = \frac{12V}{4Ω} = 3A$

Step 2 - Calculate Power Dissipation:

$$P = I^2 \times R = 3^2 \times 4 = 36W$$

Step 3 - Verify Using Alternative Power Formula: $P = \frac{V^2}{R} = \frac{12^2}{4} = \frac{144}{4} = 36W$ ✓

Example 2: Wire Resistance Calculation

Scenario: Calculate the resistance of 100 feet of 12 AWG copper wire

Given Data:

• Length: 100 feet = 30.48 meters
• 12 AWG diameter: 2.05 mm, Area: 3.31 mm²
• Copper resistivity: 1.68 × 10⁻⁸ Ω·m

Step 1 - Convert Units: Area = 3.31 mm² = 3.31 × 10⁻⁶ m²

Step 2 - Apply Resistance Formula: $R = \rho \times \frac{L}{A} = 1.68 \times 10^{-8} \times \frac{30.48}{3.31 \times 10^{-6}}$

$$R = 1.68 \times 10^{-8} \times 9.21 \times 10^{6} = 0.155Ω$$

Result: 100 feet of 12 AWG copper wire has 0.155Ω resistance

Example 3: Series Resistance Circuit

Given: Three resistors in series: 10Ω, 15Ω, and 5Ω connected to 24V source

Step 1 - Calculate Total Resistance: $R_\text{total} = R_1 + R_2 + R_3 = 10 + 15 + 5 = 30Ω$

Step 2 - Calculate Circuit Current: $I = \frac{V}{R_\text{total}} = \frac{24V}{30Ω} = 0.8A$

Step 3 - Calculate Individual Voltage Drops:

• $V_1 = I \times R_1 = 0.8 \times 10 = 8V$
• $V_2 = I \times R_2 = 0.8 \times 15 = 12V$
• $V_3 = I \times R_3 = 0.8 \times 5 = 4V$

Step 4 - Verify Kirchhoff's Voltage Law: $V_1 + V_2 + V_3 = 8 + 12 + 4 = 24V$ ✓

Example 4: Parallel Resistance Circuit

Given: Three resistors in parallel: 6Ω, 12Ω, and 4Ω connected to 12V source

Step 1 - Calculate Total Resistance: $\frac{1}{R_\text{total}} = \frac{1}{6} + \frac{1}{12} + \frac{1}{4}$

$\frac{1}{R_\text{total}} = \frac{2 + 1 + 3}{12} = \frac{6}{12} = 0.5$

$R_\text{total} = \frac{1}{0.5} = 2Ω$

Step 2 - Calculate Total Current: $I_\text{total} = \frac{V}{R_\text{total}} = \frac{12V}{2Ω} = 6A$

Step 3 - Calculate Individual Branch Currents:

• $I_1 = \frac{V}{R_1} = \frac{12}{6} = 2A$
• $I_2 = \frac{V}{R_2} = \frac{12}{12} = 1A$
• $I_3 = \frac{V}{R_3} = \frac{12}{4} = 3A$

Step 4 - Verify Kirchhoff's Current Law: $I_1 + I_2 + I_3 = 2 + 1 + 3 = 6A$ ✓

Temperature Effects on Resistance

Temperature Coefficient Calculations

Example: Copper wire resistance at different temperatures

Given: 100m of copper wire with 1Ω resistance at 20°C

At 75°C (operating temperature):

$$R_{75} = R_{20} \times [1 + 0.004 \times (75 - 20)]$$ $$R_{75} = 1 \times [1 + 0.004 \times 55] = 1 \times 1.22 = 1.22Ω$$

Impact: 22% increase in resistance due to temperature rise

Practical Temperature Considerations

Why temperature matters:

• Motor windings: Resistance increases as motors heat up during operation
• Power transmission: Line losses increase in hot weather
• Electronic components: Performance changes with temperature
• Heating elements: Designed to operate at high temperatures safely

Real-World Applications of Resistance Calculations

1. Heating Element Design

Electric water heater element calculation:

Requirements: 4500W heating element for 240V supply

Step 1 - Calculate Required Resistance:

$$R = \frac{V^2}{P} = \frac{240^2}{4500} = \frac{57,600}{4500} = 12.8Ω$$

Step 2 - Calculate Operating Current: $I = \frac{P}{V} = \frac{4500}{240} = 18.75A$

Step 3 - Verify Power Calculation: $P = I^2 \times R = 18.75^2 \times 12.8 = 4500W$ ✓

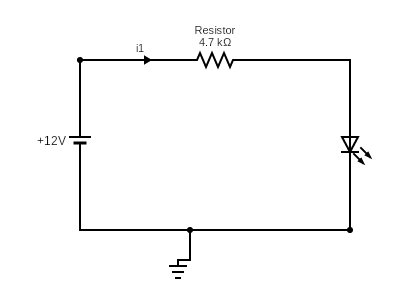
2. LED Current Limiting Resistor

Problem: Calculate resistor value for LED circuit

Given:

• Supply voltage: 12V
• LED forward voltage: 2.1V
• Desired LED current: 20mA

Step 1 - Calculate Voltage Drop Across Resistor: $V_R = V_{supply} - V_{LED} = 12 - 2.1 = 9.9V$

Step 2 - Calculate Required Resistance: $R = \frac{V_R}{I} = \frac{9.9V}{0.02A} = 495Ω$

Step 3 - Select Standard Resistor Value: Use 470Ω (closest standard value)

Step 4 - Calculate Actual Current: $I = \frac{9.9V}{470Ω} = 21.1mA$ (acceptable)

3. Voltage Drop Analysis

Scenario: 200-foot cable run for 120V, 15A load

Given: 12 AWG copper wire (1.6Ω/1000ft resistance)

Step 1 - Calculate Cable Resistance: Round trip distance: 200 × 2 = 400 feet $R_{cable} = 1.6 \times \frac{400}{1000} = 0.64Ω$

Step 2 - Calculate Voltage Drop: $V_{drop} = I \times R = 15A \times 0.64Ω = 9.6V$

Step 3 - Calculate Load Voltage: $V_{load} = 120V - 9.6V = 110.4V$

Step 4 - Calculate Percentage Drop: $\%Drop = \frac{9.6V}{120V} \times 100\% = 8\%$

Conclusion: 8% voltage drop exceeds acceptable limits (typically 3-5%), requiring larger wire size.

Advanced Resistance Concepts

AC Impedance vs DC Resistance

At higher frequencies, conductors exhibit impedance rather than simple resistance:

$$Z = R + jX$$

Where:

• Z = Impedance (ohms)
• R = Resistance (real component)
• X = Reactance (imaginary component)
• j = Imaginary unit

Skin Effect: At high frequencies, current concentrates near the conductor surface, effectively reducing the cross-sectional area and increasing resistance.

Superconductivity

Some materials exhibit zero electrical resistance below a critical temperature:

• Type I superconductors: Elements like mercury, lead
• Type II superconductors: Compounds like YBCO ceramics
• Applications: MRI magnets, power transmission research
• Limitation: Require cryogenic cooling systems

Measuring Resistance in Practice

Using a Digital Multimeter

Procedure for resistance measurement:

1. Power off the circuit completely
2. Isolate the component from the circuit
3. Select ohms range on multimeter
4. Connect probes across the component
5. Read resistance value directly

Common Measurement Errors

Error sources:

• Parallel paths: Other circuit components affecting reading
• Contact resistance: Poor probe connections
• Temperature effects: Component heating during measurement
• Range selection: Using inappropriate measurement range

Troubleshooting with Resistance Measurements

Typical resistance values:

• Good wire connections: <0.1Ω
• Heating elements: 10-50Ω when cold
• Motor windings: 1-20Ω typically
• Open circuits: Infinite resistance (OL display)
• Short circuits: Near zero resistance

Conclusion: Mastering Electrical Resistance

Understanding electrical resistance and its calculations is fundamental to working with any electrical or electronic system. From designing simple LED circuits to analyzing complex power distribution systems, resistance determines how current flows, how much power is consumed, and how components behave under different conditions.

Key principles to remember:

• Ohm's Law governs the relationship between voltage, current, and resistance
• Power dissipation increases with the square of current (P = I²R)
• Temperature significantly affects resistance in most materials
• Series circuits add resistances, parallel circuits reduce total resistance
• Material properties and physical dimensions determine resistance values

Whether you're calculating voltage drops in wire runs, selecting current-limiting resistors, or designing heating elements, these fundamental concepts and calculation methods will serve as your foundation for electrical analysis and design.

Ready to apply these concepts? Start by practicing with simple circuits and gradually work up to more complex applications. The mathematical relationships are straightforward, but the practical applications are virtually limitless.

For advanced circuit analysis techniques, explore our guides on Kirchhoff's Laws and AC circuit analysis.

---

🔗 Related Posts

• Kirchhoff's Laws: Complete Guide with Circuit Analysis Examples
• Understanding Electric Current: A Comprehensive Guide
• Complete Guide to Voltage Drop: Calculations, Tables & Calculators
• AC Capacitors: Types, Functionality, and Applications

Helpful Calculators

• Ohm's Law Calculator
• Resistor Color Code Calculator
• Series Parallel Resistance Calculator
• Voltage Drop Calculator

---

Credits

• Photo by Angeles Pérez on Unsplash